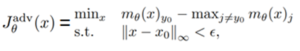“המסע הארוך ביותר נפתח בצעד הלא נכון”. (צ’ארלס כריסטופר מארק)
ברשתות נוירונים משתמשים בשיטות אופטימיזציה בשביל למזער את פונקציית ה loss. בכתבה זו נסקור שיטות אופטימיזציה שונות מ-SGD עד Adam ומעבר לו ונסביר כיצד עובדת כל אחת מהשיטות, מה החסרונות של כל שיטה ונדבר מעט על החידושים האחרונים בתחום.
מהי אופטימיזציה למזעור פונקציית ההפסד (loss function) ?
פונקציית המחיר משמעותה עד כמה המודל שלנו צודק. ככל שהערך של פונקציית ההפסד (loss) נמוכה יותר, כך המודל “צודק” יותר. מודל “צודק” משמעו מודל שהפרדיקציה במוצאו קרובה ל Ground Truth, התוצאה שאמורה להיות בהתאם לתיוגים. למשל במודל סיווג בינארי לדואר (דואר זבל=1 דואר רגיל=0) עד כמה הציון שהמודל נותן קרוב ל1 בהינתן דואר זבל ו0 בהינתן מייל רגיל.
לכל אורך אימון המודל מטרתינו לעדכן את המשקלים (המשתנים הפנימיים של המודל) ככה שהפרדיקציה שלו תהיה קרובה יותר ל Ground Truth וזאת אנו עושים ע”י כך שגוזרים את פונקציית המחיר (מחשבים gradient) ביחס למשקלי המודל. הנגזרת מלמדת אותנו על ההתנהגות (עליה\ירידה) של הפונקציה אותה גוזרים. כיוון הגרדיאנט בנקודה מצביע על הכיוון בו הפונקציה עולה ובכיוון הנגדי יורדת מהנקודה בה אנחנו נמצאים. מטרה תהליך האימון היא למצוא ערך מינימום של פונקציית ההפסד ולשם כך משתמשים בשיטות אופטימיזציה.
Gradient Descent
שיטת האופטימיזציה המוכרת ביותר ברשתות נקראת Gradient Descent או Batch Gradient Descent. בשיטה זו, אנחנו מחשבים את כיוון הגרדיאנט מהנקודה שבה אנחנו נמצאים (משקלי הרשת) בהתאם לפונקציית ההפסד, ומתקדמים מהנקודה הנוכחית בצעד קטן בכיוון הנגדי לכיוון הגרדיאנט. כיוון הגרדיאנט הוא הכיוון בו ערך הפונקציה עולה בצורה מקסימלית, הכיוון הנגדי הוא הכיוון בו הפונקציה הכי יורדת.
לדוגמה לחישוב Gradient descent עבור מודל רגרסיה לינארית n מימדית:
עבור קלט וקטור x, וקטור y שהינו ה Ground Truth (התחזית הרצויה) ו θ
וקטור הפרמטרים של מודל הרגרסייה.
ההיפותזה של התחזית עבור קלט x נראית כך:
מייצגת את התחזית עבור דוגמא x
בהינתן m דגימות פונקצית ההפסד תראה כך:
הגרדיאנט:
הוא פרמטר המייצג את גודל הצעד שנלקח בצעד העדכון learning rate
עבור learning rate נקבל שצעד העדכון הייה:
כלומר אנחנו מחשבים את הגרדיאנט של פונקציית ההפסד לפי הנתונים באימון, עושים צעד מערך המשקולות הנוכחיים בכיוון הנגדי לכיוון הגרדיאנט, ומעדכנים את המשקלות לערך החדש. גודל הצעד נקבע לפי ה learning rate
בפועל חישוב הגרדיאנט לפי כל סט האימון (גודל batch ענקי) לוקחת זמן רב ולא ישים מבחינה חישובית. לעומת זאת SGD=Stochastic Gradient Descent, היא שיטה לפיה עוברים בלולאה מספר פעמים (כמספר ה-epochs) על סט האימון, ובכל איטרציה במקום לחשב את הגרדיאנט לפי כל סט האימון, מחשבים את הגרדיאנט לפי הדוגמא הנוכחית. (זהו למעשה batch בגודל אחד)
כדי לגרום לגרדיאנטים להיות פחות תנודתיים, במקום לחשב גרדיאנט לפי קלט יחיד, מחשבים לפי קבוצה קטנה של קלטים, שיטה זו נקראת Mini Batch Gradient Descent.

אפשר לראות בתמונה שחישוב הגרדיאנט בכל צעד על בסיס batch גדול יותר מביא להתכנסות יציבה יותר.
ללא קשר לגודל ה Batch לשיטת ה-SGD יש לא מעט בעיות:
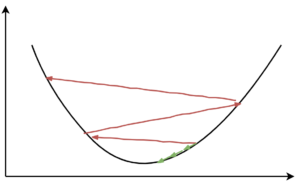
1.אם יש כיוון בו פונקציית ההפסד משתנה מהר והכיוון בו הגרדיאנט משתנה לאט, נוצר מצב שהצעדים נעשים בזיגזגים וההתכנסות נהיית איטית.

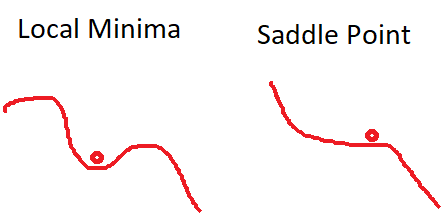
- התכנסות למינימום מקומי ולנקודות אוכף. כאשר SGD מגיע למינימום מקומי, או נקודת אוכף הגרדיאנט שווה ל0 וSGD יעצר. במימד גבוה זו סיטואציה שכיחה, למעשה הרבה יותר ממינימום מקומי. מסיבה זו הבעיה העיקרית היא עם נקודות אוכף ופחות עם מינימום מקומי. בעיה זו נוצרת גם בסביבת נקודת האוכף, שבה גרדיאנט מאוד קטן, וזו בעיה גדולה.
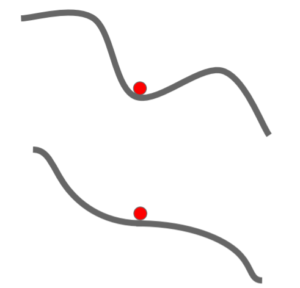 מקור
מקור - כיוון הגרדיאנט עלול לסבול מרעשים בעקבות העבודה עם mini batch, לדגימות חריגות (outliers) ב-Batch יכולה להיות השפעה חזקה.למרבה המזל יש אסטרטגייה פשוטה שעובדת טוב ברוב המקרים כדי להתמודד עם בעיית תנודתיות הגרדיאנטים והעצירה בנקודות אוכף.
הוספת מומנטום ל-SGD
מומנטום, הוא עיקרון שמגיע ממכניקה, תנועות של גופים בעולם הפיזי לרוב חלקות ולא נוטות לזגזג מפני שהן צוברות מהירות מהצעדים הקודמים שלהן. הרעיון של הוספת מומנטום ל-SGD הוא להוסיף את המהירות הכיונית מהצעדים הקודמים לצעד הנוכחי ובכך למצע את כיווניות הגרדיאנט.
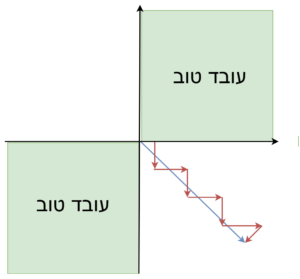
SGD עם מומנטום כמעט תמיד עובד מהר יותר מאשר SGD. הרעיון הבסיסי הוא לחשב ממוצע משוקלל של היסטוריית הגרדיאנטים, ולהשתמש בהם כדי לעדכן את המשקלים במקום. הוספת המומנטום תחליק את צעדי הגרדיאנט. לדוגמא אם צעדי ה-SGD נראים כך:
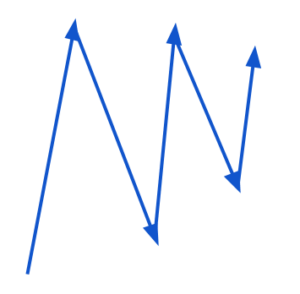
אם ניקח את ממוצע כיווני הגרדיאנט בצעדים הקודמים, ערך הגרדיאנט בצירים שבהם יש שונות גדולה בערכי הגרדיאנטים אזי מיצוע הערכים יקטין את ערך הגרדיאנט בכיוניות הזו, והערך בצירים שבהם כל הגרדיאנטים מצביעים לאותו כיוון יגדל (סכום). הוספת המומנטים מקטינה את התנודתיות של הגרדיאנטים.
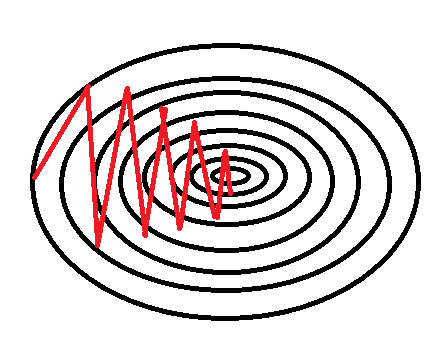
הוספת המומנטום תעזור לנו גם לצאת ממינימום מקומי ונקודות אוכף, בעזרת התנופה מהגרדיאנטים הקודמים.

לרוב בוחרים את rho להיות 0.9 או 0.99.
שיטת אופטימיזציה שנועדה כדי להתמודד עם הזיגזוג שנוצר כתוצאה מהמקרה בו גרדיאנט משתנה בעוצמה שונה בכיוונים שונים היא AdaGrad.
AdaGrad
הרעיון של AdaGrad הוא שבזמן תהליך האופטימיזציה, אנחנו נשמור סכום רץ של כל ריבועי הגרדיאנטים שאנחנו רואים במהלך האימון. כאשר נרצה לעדכן את הגרדיאנט שלנו, נחלק את הערך שלנו בסכום ריבועי הגרדיאנטים.
מה יקרה כתוצאה מהחילוק בהנחה שיש לנו קואורדינטה אחת שהנגזרת הכיוונית שלה תמיד קטנה קואורדינטה אחרת שהנגזרת הכיוונית שלה תמיד גדולה?

הקואורדינטה עם הנגזרת הקטנה תחולק במספר קטן ולכן ההשפעה שלה על כיון הצעד תגדל, ואילו עבור הקואורדינטה עם הנגזרת הכיונית הגדולה, ההשפעה שלה תלך ותקטן כי היא תחולק במספר גדול. העיקרון של AdaGrad הוא ליצור אדפטציה, שוויון בין כיוונים שונים, קצב הלימוד משתנה אדפטיבית.
מה קורה לAdaGrad לאורך תהליך האימון כאשר סכום הריבועים הולך וגדל?
גודל הצעדים (learning rate) יקטן לאורך הזמן, כי אנחנו ממשיכים להגדיל את סכום הריבועים. במקרה הקמור (convex) , שיש בו מובטח מינימום יחיד, התיאוריה אומרת שזה למעשה ממש טוב. כי במקרה הזה כאשר מתקרבים למינימום רוצים לעשות צעדים קטנים יותר כדי לא להחמיץ את המינימום. לעומת זאת המקרה הלא קמור זה קצת בעייתי. כי אנחנו עלולים להיתקע בנקודת אוכף. בפרקטיקה AdaGrad לא כל כך שימושי בגלל הנטייה שלו להיתקע.
יש וריאציה קלה לAdaGrad שמתמודדת עם הבעיה הזו הנקראת RMSProp
RMSProp
באלגוריתם הזה במקום לתת לסכום הריבועים לגדול לאורך האלגוריתם, אנחנו מאפשרים לסכום ריבועי הגרדיאנטים לקטון. ב-RMSProp , אחרי שאנחנו מחשבים את הגרדיאנטים שלנו, אנחנו לוקחים את הערכה הנוכחית שלנו של ריבועי הגרדיאנטים, מכפילים אותה בקצב הדעיכה,לרוב 0.9 או 0.99, ומוסיפים לו 1 פחות קצב הדעיכה כפול ריבוע הגרדיאנט הנוכחי.

הקורא הדקדקן שישווה בין Ada-Grad לבין RMSProp יבחין שאם נחליף במשוואות של RMSProp את הממוצע המשוכלל לפי פרמטרdecay_rate לסכום, כלומר להחליף את decay_rate ב-1 ואת 1-decay_rate ב-1 נקבל בדיוק את AdaGrad.
RMSProp שומר על המאפיין הנחמד של Ada-Grad להאיץ מהירות לאורך כיוון אחד ולהאט אותה בכיוון אחר, מבלי הבעיה של תמיד להאט.
ניתן לראות ש RMSProp לא עושה overshoot והוא נע בכיוון יחסית שווה לאורך כל המימדים.
ראינו שלמומנטום יש את העיקרון של המהירות שדוחפת אותו, וראינו רעיון אחר עם RMSProp ו Ada-grad של חישוב סכום ריבועי הגרדיאנטים וחלוקה בהם. שני הרעיונות האלו נראים טובים בפני עצמם. השאלה המתבקשת היא:
למה לא גם וגם ? ? ?
Adam
משלב את השיטות הקדמות Momentum+ AdaGrad

אבל בצורה הזו הוא סובל מבעיה בצעדים הראשונים. המומנט השני מאותחל ל-0, אחרי איטרציה בודדת המומנט השני המומנט השני עדיין ממש קרוב ל-0 בהנחה ש bata1 שווה ל-0.9 או 0.99. אז כאשר נבצע חילוק במומנט השני, זה יגרום לכך שנבצע צעד מאוד גדול על ההתחלה. כדי לפתור את הבעיה הזו הוסיפו לAdam שינוי קטן.

המשתנים first_unbias ו second_unbias מתנהגים כמו המומנט הראשון והשני. כאשר t גדול וכאשר t קטן, השינוי של ה-unbias מקטין את first_unbias ו second_unbias ביחס למומנטים, אבל היות ובחישוב x אנחנו מפעילים שורש על second_unbias, נראה שיחס הגדלים בין המונה למכנה קטן, וכך גם צעדי ההתחלה.
פרמטרים מומלצים לAdam: bata1=0.9, bata2=0.999 ,learning_rate=1e-3
מה החסרונות של Adam וכיצד מתמודדים איתם?
למרות שAdam הוא אחד משיטות האופטימיזציה השימושיות ביותר כיום, הוא סובל מ 2 בעיות עיקריות:
- האימון הראשוני של Adam לא יציב, בגלל שבתחילת האימון יש מעט נקודות לחישוב הממוצע עבור המומנט השני. צעדים גדולים מבוססים על מידע מועט ורועש יכולים לגרום להשתקעות בנקודת מינימום מקומית או אוכף. בעיה המשותפת לרוב אלגוריתמי אופטימיזציה.
- המודל המתקבל לא מכליל בצורה טובה (נוטה ל overfitting) ביחס לSGD עם מומנטום.
דרך אחת להתמודד עם הבעיה הראשונה היא להתחיל לאמן בקצב נמוך, וכאשר המודל מתגבר על בעיית ההתייצבות הראשוניות, להגביר את הקצב. שיטה זו נקראת learning rate warm-up. חסרונה של השיטה הוא שמידת החימום הנדרש אינה ידועה ומשתנה מערך נתונים למערך נתונים.
במקום שנגדיר בעצמנו את הפרמטרים עבור ה-warm-up ניתן להשתמש ב-RAdam .RAdam הוא אלגוריתם חדש שמחליף את ה-warm-up ב-Adam ולא מצריך הגדרת פרמטרים עבור תקופת החימום. חוקרים שפתחו את RAdam מצאו כי בעית ההתיצבות הראשונית נגרמת כתוצאה משונות לקויה ב-learning rate האדפטיבי כתוצאה מכמות הנתונים המוגבלת בתחילת האימון. הדרך בה (Rectified Adam)-RAdam פותר את הבעיה היא על ידי תיקון (Rectified) השונות של ה-learning rate האדפטיבי על סמך הגרדיאנטים.
אחת השיטות כדי להתגבר על הבעיה השנייה היא להתחיל עם Adam ולהחליף ל SGD כאשר קריטריונים מסוימים מגיעים. בדרך זו ננצל את ההתכנסות המהירה של Adam בתחילת האימון, ואת יכולת ההכללה של SGD. דרך נוספת היא שימוש באופטימיזרים שמשלבים את הטוב משני העולמות כמו AdaBound, PADAM ו-SWATS.
כל השיטות שהזכרנו הינן שיטות מסדר ראשון, מסתמכות רק על הנגזרת. ישנן שיטות מסדר שני שמסתמכות גם על הנגזרת השנייה בקביעת הצעד. בשיטות אילו אין צורך לקבוע את ה-learning rate, אבל הן אינן ישימות עבור למידה עמוקה כי הן לוקחות זמן ריבועי במספר המשקולות.
איך בוחרים learning rate?
בכל האלגוריתמים שהצגנו נדרשנו לקבוע את ה-learning rate. בחירת learning rate גבוהה מידי יכול לגרום להתבדרות, או התכנסות למינימום מקומי, ו-learning rate נמוך מידי יקח זמן רב להיכנס.
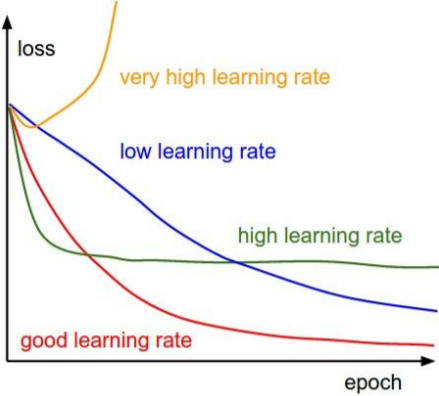
לא חייבים לדבוק באותו learning rate לאורך כל האימון. מומלץ לרוב להקטין את ה-learning rate לאורך האימון ובכך לשלב בין היתרונות של קצב לימוד מהיר ואיטי. הקטנת ה -learning rate מקובלת לרוב בשימוש ב-SGD ופחות באלגוריתמים אדפטיבים שבהם שינוי ה-learning rate כבר נמצא באלגוריתם. בנוסף learning rate נמוך בתחילת האימון, warm-up, יכול להועיל, כפי שציינו קודם.
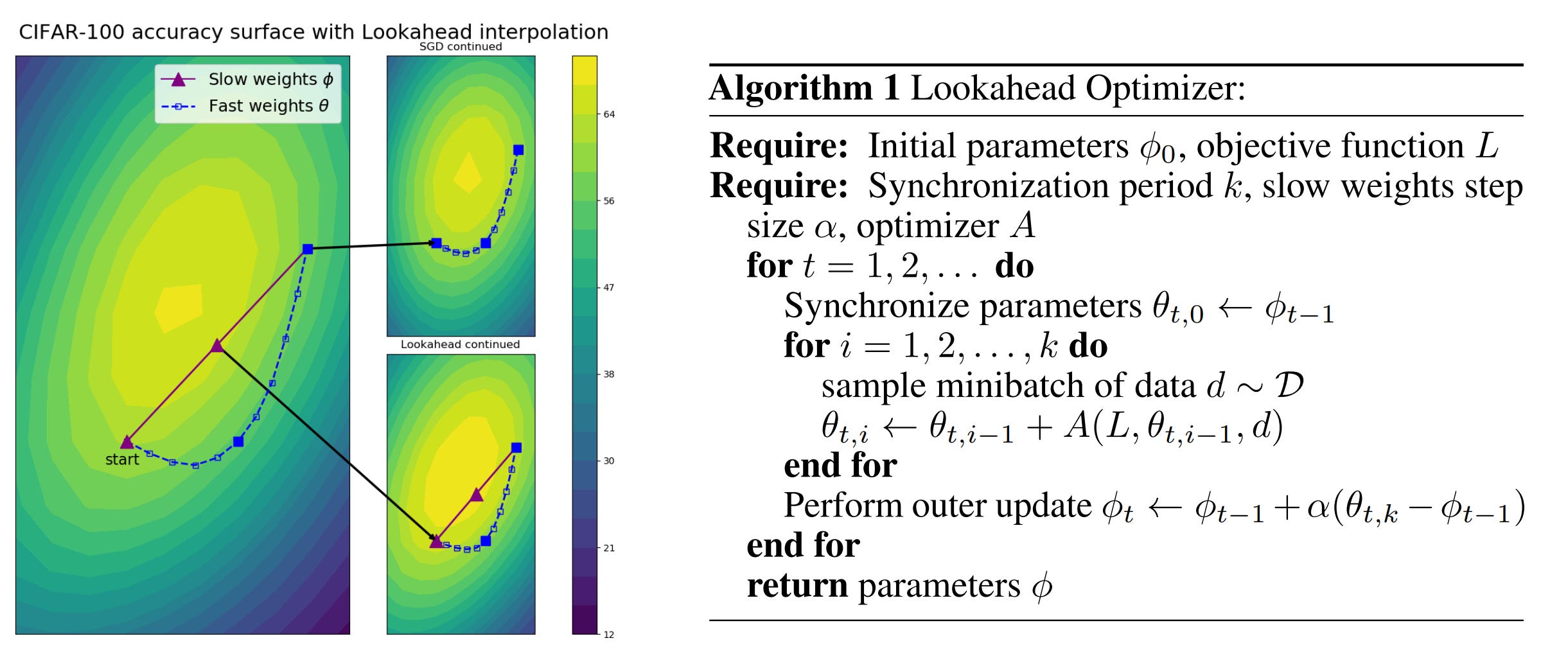
LookAhead
חידוש נוסף שיצא לאחרונה בתחום האופטימייזרים הוא LookAhead אלגוריתם ש”מתלבש” מעל אופטימייזרים קיימים ושמשפר את יציבות הלמידה, מוריד את השונות של האופטימייזר עליו הוא מתלבש, מתכנס מהר יותר ובנוסף מפחית את הצורך בכיוונון מוקפד של היפר-פרמטרים. LookAhead שומר על שתי קבוצות משקולות ומשתלב ביניהם (מבצע אינטרפולצייה) – משקולות מהירות שמסתכלות קדימה וחוקרות את השטח ומשקולות האיטיות נשארות מאחור ומספקות יציבות. לאחר מספר צעדים חקרניים המשקולות האיטיות מתקדמות בכיוון המשקולות המהירות בצעד קטן, והמשקולות המהירות מתחילות להתקדם מהמקום החדש של המשקולות האיטיות. הצעדים החקרנים (המהירים) נקבעים על ידי האופטימייזר הפנימי עליו LookAhead מתלבש.
במה משתמשים בפועל?
נכון להיום השיטות הנפוצות ביותר הם Adam שמתכנס מהר ו-SGD עם מומנטום ו-learning rate decay משמש בדרך כלל עבור SOTA אבל דורש fine tuning. בין השיטות החדישות היום שנותנות תוצאות טובות ניתן למצוא את Ranger אופטימיזר שמשלב את RAdam עם LookAhead. כל אחד מהם מטפל בהיבטים שונים של אופטימיזציה. RAdam מייצב אימונים ההתחלתיים, ו-LookAhead מייצב את האימונים הבאים, מבצע אקספלורציה מזרז את תהליך ההתכנסות.
ספרו לנו בתגובות באילו שיטות אופטימיזציה אתם משתמשים, ומה עבד לכם טוב?
שאלות אפשריות לראיונות עבודה:
איך עובד backpropagation?
אילו שיטות אופטימיזציה לאימון רשתות אתה מכיר?
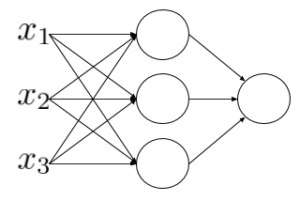
כיצד משתמשים ב-SGD לאימוני רשת עצבית?
מה היתרונות בשימוש במיני באצ’ים ב-gradient descent?
איך עובד Adam? מה ההבדל העיקרי בינו לבין SGD?
למה לעיתים קרובות ל-Adam יש לוס נמוך יותר אבל SGD נותן תוצאות יותר טובות על ה-test ?
מה זה learning rate?
מה קורה כשה-learning rate גדול מדי? קטן מדי?
מה עדיף learning rate קבוע או משתנה לאורך האימון?
איך מחליטים מתי להפסיק לאמן רשת עצבית?
מה זה model checkpointing?
חומר נוסף:
Gradient Descent Intuition Andrew Ng