אנחנו חיים במציאות שבה אלגוריתמי Machine Learning כבר חלק בלתי נפרד מחיי היום יום שלנו. עם זאת, רוב הפיתוח שלהם נעשה בהנחה שאין סוכן זדוני שמטרתו להכשיל אותם, דבר שניתן לעשות בקלות. נכון להיום יותר קל לבנות מערכות תוקפות מאשר מערכות המגינות מפני תקיפה זדונית. יתרה מזאת, לא הוכח שניתן להגן מפני כל מתקפה, או לחלופין, שכמו בקריפטוגריפה ימצא יתרון לצד המתגונן¹.
חלוקה לסוגי תקיפות
תקיפה דיגיטלית משמעותה לעשות מניפולציה של הקלט שניתן למודל כדי שיגיב בצורה שגויה. תקיפה פיזית משמעותה לעשות מניפולציה שתשפיע על חיישן שמנטר את הסביבה למשל.
נהוג להבדיל בין שני סוגי התקפות דיגיטליות²:
א) קופסה לבנה – לתוקף יש מידע מלא לגבי אלגוריתם האימון, ארכיטקטורת המודל, המשקולות של המודל וכל הפרמטרים שלו.
ב) קופסה שחורה – לתוקף אין שום ידע או שיש לו ידע מוגבל על המודל. אם יש לתוקף גישה לתת למודל קלט ולחלץ פלט אז הוא מרוויח עוד מידע.
במאמר זה אספר על שלושה אפיקי התקפה שונים שמטרתם להכשיל Deep Neural Networks שמאומנות על ידי מאגרי תמונות מוכרות כגון MNIST, CIFAR ו-ImageNet: התקפות מבוססות גרדיאנט, התקפות מבוססות על אוגמנטציה מרחבית והתקפות גבול.
1) התקפות מבוססות גרדיאנט
בהתקפות אלו יש גישה לכל המידע הדרוש (קופסה לבנה). בהתקפות כאלו נעשה שימוש באופטימיזציה איטרטיבית בעזרת גרדיאנט. זאת במטרה למצוא הפרעה (Perturbation) מינימלית לקלט שיביא לניבוי מחלקה (Class) שגוי על ידי המודל המתגונן.
שיטת Projected Gradient Descent- PGD
בשיטה זו מאמנים יצירת קלט זדוני x (כזה שיכשיל את המודל המותקף) באופן איטרטיבי. תהליך האימון מבוסס על כך שלוקחים גרדיאנט של פונקציית ההפסד (תוסבר בהמשך) וכל איטרציה מכפילים בפרמטר α הגדול מ-0 שהוא ה – learning rate כמו ב BackPropogation-

כדי לייעל את התהליך לא מחפשים בכל מרחב הקלט, אלא רק בסביבה של הנקודות x במרחק 𝛆 מ- (מרחק הגדול מ-0). סביבה זו מיוצגת על ידי ההיטל –
ל-
. מעדכנים את הקלט הזדוני x, כאשר הקלט מאותחל להפרעה רנדומלית בתוך הסביבה הזו³-
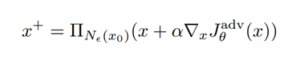
פונקציית ההפסד של שיטת PGD
פונקציית ההפסד מטרתה למדוד עד כמה הקלט הזדוני מביא לידי תגובה רצויה למודל המותקף. הפונקציה מוגדרת כ³-
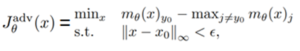
הביטוי הינו ערך פונקציית הלוגיט המקסימלי כאשר ϴ הם פרמטרי המודל – m ו- j אינה המחלקה התואמת ל-label ה-
של הקלט הזדוני x.
פונקציה ההפסד רוצה להקטין את ההפרש בין ערך פונקציית הלוגיט המקסימלי לבין ערך פונקציית הלוגיט של ה-Label של הקלט הזדוני x –
.
בנוסף, 𝛆 תוחם את נורמה ה – ∞ של ההפרש בין כל נקודה של הקלט הזדוני לקלט המקורי (ראו כתבה קצרה המסבירה על הנורמות השונות⁴).
לדוגמה –
במצב בינארי, נניח כי קיימת תמונה של חתול . המחלקה של חתול מקבלת ערך לפי פונקציית הלוגיט
. המחלקה של כלב (j) מקבלת ערך
. כלומר, לפי ערכי פונקציית הלוגיט, התמונה בעלת סיכוי יותר גבוה להיות תמונה של כלב. במצב הנתון קיים רק ערך (j) אחד שמייצג מחלקה שאינה חתול ולכן הוא יהיה מקסימלי לפי –
. הפונקציה תמיד תיתן תוצאה שלילית כאשר קיים ניבוי מחלקה שגוי, כפי שניתן לראות גם בדוגמה
. כך, על ידי הפחתת פונקציית ההפסד עוד ועוד, נלמד כיצד למצוא הפרעה זדונית שתביא לניבוי מחלקה שגוי בהסתברות הולכת וגדלה.

ישנם עוד שיטות דומות ל-PGD, כמו BIM – Basic Iterative Method וכמו Fast gradient sign method – FGSM. ההבדל היחיד² בין PGD ל – BIM הוא תנאי ההתחלה. לעומת זאת FGSM דומה לשתי השיטות האלו אך אינה איטרטיבית ומקבלת תוצאות סבירות בצעד אחד גדול².
במצבים בהם לא ניתן לקחת גרדיאנטים או שהם אינם עוזרים להתקפה ניתן לקרב אותם בעזרת שיטות סטוכסטיות. ניתן לעשות זאת בעזרת שיטה מוצלחת הנקראת SPSA – Simultaneous Perturbation Stochastic Approximation:

הדבר החשוב לזכור: השוואה בין SPSA לבין PGD מראה כי אין הבדל משמעותי בתוצאות, ובמקרים מסוימים SPSA יכולה להתכנס לנקודת מינימום יותר טובה³.
2) התקפות מבוססות על אוגמנטציה מרחבית
בהתקפות אלו יש גישה רק להחלטה הסופית של המודל (קופסה שחורה), אבל דרוש לתת למודל קלט ולחלץ פלט. שינוי פשוט של הקלט על ידי סיבובו או הזזה שלו (Translation) יכולים בקלות לגרום למודל לבצע ניבוי שגוי. אחת השיטות לבצע התקפה כזאת היא על ידי חיפוש (Grid Search) של מרחב הפרמטריזציה של ההתקפה לצורך מציאת משתנה שיביא לניבוי מחלקה שגוי על ידי המודל המתגונן. ניתן להשתמש בעוד שיטות כמו גם בחיפוש מבוסס גרדיאנט למציאת סיבוב והזזה זדוניים:

3) התקפות גבול
בהתקפות אלו יש גישה רק להחלטה הסופית של המודל (קופסה שחורה), אבל דרוש לתת למודל קלט ולחלץ פלט. התקפה זו מאותחלת למצב שבו ישנה הפרעה (Perturbation) גדולה. לאחר מכן, על ידי אופטימיזציה איטרטיבית המבוססת על הילוך מקרי (Random Walk), ההתקפה בוחנת את הגבול שבין ניבוי שגוי לניבוי נכון כך שעדיין נשארת זדונית אבל מתקרבת ככל שניתן לניבוי מחלקה נכון. כתוצאה מכך היא בעצם מקטינה את ההפרעה בצורה איטרטיבית. על ידי צעדים רנדומליים הנבחרים מהתפלגות נורמלית ניתן להתכנס לפתרון שיתן קלט שיהיה מסווג על ידי המודל המתגונן בצורה שגויה:

סיכום
בגלל הכמות הבלתי מוגבלת של קלט שניתן ליצור, מאוד קשה לבנות הגנה המסתגלת לסוגים שונים של התקפות¹. לדוגמה, נמצא שלהגנות מסוימות המתמודדות יפה עם התקפה מבוססת גרדיאנט אין רובסטיות להתמודד עם אוגמנטציה מרחבית ושניהם יחד יוצרים התקפה שמכשילה עוד יותר את המודל המתגונן⁵.
אם החזקתם מעמד עד כאן אז הגעתם לפסקה הכי חשובה. בימים אלו מתחילה תחרות נושאת פרסים⁷ בנושא שעליו קראתם. בשלב הראשוני, על המתמודדים שבונים הגנה יש תחילה להתמודד מפני שלוש ההתקפות שתיארתי כאן. אז אני מזמין אתכם להצטרף אלי בפיתוח הגנה או מתקפה. התחרות תיגמר רק כאשר תמצא הגנה שלא נותנת אף ניבוי מחלקה שגוי ל-90 יום.
קישורים:
¹ http://www.cleverhans.io/ – Cleverhans blog
² https://arxiv.org/pdf/1804.00097.pdf – Adversarial Attacks and Defences Competition
https://arxiv.org/pdf/1802.05666.pdf – Adversarial Risk and the Dangers of Evaluating Against Weak Attacks ³
medium.com/@montjoile/l0-norm-l1-norm-l2-norm-l-infinity-norm-7a7d18a4f40c ⁴
https://arxiv.org/pdf/1712.02779.pdf – A Rotation and a Translation Suffice: Fooling CNNs with Simple Transformations⁵
https://arxiv.org/pdf/1712.04248.pdf – Decision-Based Adversarial Attacks: Reliable Attacks Against Black-Box Machine Learning Models ⁶
⁷ https://github.com/google/unrestricted-adversarial-examples



