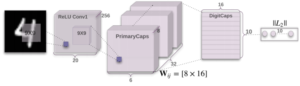
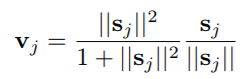geoffrey hinton

Jun

2018

העמקה לרשת הקפסולות Dynamic Routing Between Capsules – תיאוריה

מיועד ל- מטיבי לכת (כתבה מאוד טכנית)

בכתבה זו מטרתי להסביר את התיאוריה שבמאמר “Dynamic Routing between Capsules”. למי שלא מכיר את ההקשר ממליץ לקרוא קודם את הרקע בכתבה הזו: “הרעיון מאחורי רשת הקפסולות” שמסבירה את המאמר המוקדם יותר של הינטון: “Transforming Auto-“encoders. (אם כי אפשר להבין גם הכול מכתבה זו בלבד)

נציין שעל אף שהרעיון מעניין ונשמע מבטיח, הוא בינתיים הוכח כמנצח רק על מאגר תמונות ספרות וגם על ספרות חופפות מ MNIST. (ז”א תמונה המכילה כמה ספרות זו על זו). יתרון משמעותי נוסף שיש לארכיטקטורה זו היא ההסתפקות ב database קטן, וחסרון הוא משך אימון ארוך.

תיאוריה

אם עלי לתת את כל התורה על רגל אחת אגיד על דרך המשל:
על ההורים לקבל החלטות כבדות משקל בחיים ועל הילדים לקבל החלטות פשוטות. כל הורה מקבל את החלטותיו לפי דעת הרוב של ילדיו, כאשר כל ילד “מומחה” בנישה קטנה אחרת. ההורים למשל עשויים להחליט לעבור למושב אחרי שראו ששנים משלושת ילדיהם אוהבים טבע.
ולהקשר הזיהוי תמונה: אוביקט בתמונה מורכב מהרבה אלמנטים. זיהוי של כל אלמנט ומאפייניו (למשל גודלו ומיקומו היחסי) יכול להעיד על קיום האוביקט כולו בתמונה.
האוביקט בתמונה מיוצג במבנה עץ שכל קודקוד הוא קפסולה שיש לו בנים ואב. שכבה של קפסולות הינן קפסולות מאותו הדור. כל קפסולת בן מנבאת מה תגיד קפסולת אביו. למשל בתמונת פנים קפסולה שמזהה אלמנט עין שאביה הינו קפסולה המזהה אלמנט פנים, תעיד על פנים במיקום זה או אחר בהסתברויות גבוהות. הסכמה בין קפסולות מאותה שכבה לגבי דיעת האב תכריע את דיעת האב. אמחיש את הרעיון באיור הבא:

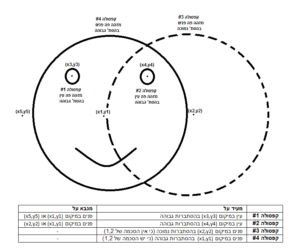
capsules demo

איור זה מדגים זיהוי פנים עם שתי שכבות קפסולות. שכבה של קפסולות שמיומנות בלזהות עיניים ושכבה גבוהה יותר של קפסולות שמיומנות בלזהות פנים. ניתן להמשיך את הדוגמה הזו עם עוד שכבות: למשל שכבה נמוכה יותר של קפסולות שמיומנות בלזהות עיגולים והן תעזורנה לקפסולות שמזהות עיניים. או שכבה עליונה יותר שמיומנת בלזהות אנשים ונעזרת בשכבה שמתחתיה שמיומנת בלזהות פנים.
אגב, אחד היתרונות של שיטה זו היא בזיהוי אוביקטים חופפים וזאת כי אז יש צורך בהסכמה הדדית בין כל הקפסולות כדי להחליט מהו האוביקט\ים הכולל שרואים בתמונה.

אז מהן בדיוק קפסולות ?

קפסולות הם יחידות אבסטרקטיות (בהמשך, בחלק הפרקטי נראה מימוש) שמקבלות וקטורים ומחזירות וקטורים.

כל קפסולה מחזירה:

1. וקטור מוצא שלה (*) – שגודלו מעיד על ההסתברות לקיומו של האלמנט וכיוונו מקודד את המאפיינים שלו.

2. וקטורי פרדיקציה בעבור כל אחת מהקפסולות בשכבה הבאה.

המשמעות של וקטורי הפרדיקציה הינם: מה לדעת קפסולה i יהיה המוצא של קפסולה j. אם נניח קפסולה i מומחית בזיהוי עיגולים ומזהה בהסתברות גבוהה עיגול בקורדינאטה (x3,y3) בתמונה, אז תנבא שקפסולה משכבה גבוהה ממנה שאחראית על זיהוי פנים תוציא כפלט פנים במיקום (x1,y1) .

כל קפסולה מקבלת:

1. וקטורי פרדיקציה מכל אחת מהקפסולות שבשכבה שלפניה. אם אין שכבה מלפניה (כי זו השכבה הראשונה) אז מקבלת קלט כלשהוא, למשל במימוש המוצע כפי שנראה בהמשך מקבלת תוצאה של שכבת קונבולוציה. (פיצ’רים של התמונה המקורית)

(*) – וקטור תוצאה של קפסולה הינו שיקלול חכם ומנורמל של וקטורי הפרדיקציה מכל הקפסולות בשכבה שלפניה. השיקלול הזה מתואר באלגוריתם Dynamic Routing.

מהו אלגוריתם Dynamic Routing

וקטור מוצא של קפסולה הינו סכום משוקלל של וקטורי הפרדיקציה שהגיעו מהקפסולות שבשכבה הקודמת.
השיקלול ממומש באמצעות אלגוריתם Dynamic Routing ומהותו עידכון המשקלים\מקדמי צימוד (של כל אחד מאותם וקטורי פרדיקציה) באופן איטרטיבי לפי מידת ה-“הסכמה” בין וקטור פרדיקציה כלשהוא לבין וקטור התוצאה (כפי שהוא באיטרציה הנוכחית). ככל שוקטור פרדיקציה כלשהוא תואם לכיוון של וקטור התוצאה כך יגדל המקדם\המשקל שלו. מידת התאימות מחושבת ע”י מכפלה סקלרית בינהם. (הרי מכפלה סקלרית בין וקטורים בעלי אותו כיוון הינה 1 ואחרת אם הם בכיוונים שונים פחות מ-1)

תיאור האלגוריתם בין שכבת קפסולות l לבין השכבה הבאה l+1 בעבור r איטרציות ניתוב (routing):

קלט: וקטורי הפרדיקציה של כל אחת מקפסולות i מהשכבה l לכל אחת מהקפסולות j בשכבה l+1: $\widehat{u}_{j|i}$

פלט: וקטור המוצא של כל קפסולה j משכבה l+1 : $v_{j}$

האלגוריתם:

בהתחלה אפס את כל מקדמי הצימוד $b_{i,j}$

בצע r איטרציות את שתי הפעולות הבאות: (שיקלול וקטור מוצא + עידכון משקלים)

1. $v_{j}=squash(\Sigma_{i}c_{ij}\widehat{u}_{j|i})$

כאשר מקדמי הצימוד בין הקפסולות מנורמלים באופן הבא:

$c_{i}=softmax(b_{i})=\frac{e^{b_{i}}}{\sum_{k}e^{^{b_{k}}}}$

2. עדכן את מקדמי הצימוד לפי מידת ההסכמה (המכפלה הסקלרית) בין וקטורי הפרדיקציה לוקטור התוצאה:

$b_{ij}=b_{ij}+\widehat{u}_{_j|i}\cdot v_{j}$

סוף!

כעת אם ברצונך להבין את פרטי המימוש ואת הארכיטקטורה המוצעת במאמר, עבור לכתבה:

“העמקה לרשת הקפסולות Dynamic Routing Between Capsules – פרקטיקה“

Jun

2018

העמקה לרשת הקפסולות Dynamic Routing Between Capsules – פרקטיקה

מיועד ל- מטיבי לכת (כתבה מאוד טכנית)

נכתב על ידי תמיר נווה

בכתבה זו מטרתי להסביר באופן מפורש ומספיק מפורט עד כדי שהקורא החרוץ יידע לממש בעצמו את המאמר “Dynamic Routing between Capsules”. למי שלא מכיר את ההקשר ממליץ לקרוא קודם את הרקע בכתבה הזו: “הרעיון מאחורי רשת הקפסולות” שמסבירה את המאמר המוקדם יותר של הינטון: “Transforming Auto-encoders. ואז את הכתבה הזו: “העמקה לרשת הקפסולות Dynamic Routing Between Capsules – תיאוריה” שמסבירה על התיאוריה שבמאמר.

פרקטיקה

המאמר מציע מימוש ספציפי לרעיון זה על פי ארכיטקטורה שמיועדת לזיהוי ספרות MNIST. אשתמש בסימונים המופיעים במאמר ואסביר את הארכיטקטורה.

נשים לב כי באופן כללי אלגוריתם Routing פועל בין כל שתי שכבות קפסולות סמוכות אך במימוש המוצע הוא פועל רק פעם אחת כי יש סה”כ 2 שכבות של קפסולות.

להלן התרשים של מבנה הרשת במאמר: (חייב להגיד שלקח לי זמן רב להבין ממנו מה באמת קורה באלגוריתם, מקווה שאצליח לחסוך לכם זמן זה…)

תודה ל Dynamic Routing between Capsules

הסבר על כל בלוק:

בלוק הכי שמאלי: הרשת מקבלת תמונה (של ספרה) בגודל 28×28
בלוק ReLU Conv1: שכבת קונבולוציה שהינה 256 פילטרים בגודל 9×9 ב stride=1 עם אקטיבציית Relu. לכן הטנזור במוצא בגודל 20x20x256.
בלוק PrimaryCaps: שכבת קונבולוציה שהינה 256 פילטרים בגודל 9×9 ב stride=2 עם אקטיבציית Squash (*). לכן הטנזור במוצא בגודל 6x6x256. אותו טנזור בגודל 6*6*256 אלמנטים מסודר כ 32 טנזורים בגודל 6x6x8. כל אחד מבין ה 32x6x6 וקטורים בגודל 8 כל אחד יסומן $u_{i}$
בלוק DigitCaps: שכבת Fully Connected שממומשת ע”י מטריצה W שהופכת כל אחד מה 6x6x32=1152 וקטורי $u_{i}$ לעשרה וקטורי (פרדיקציה) $\widehat{u}_{j|i}$ בגודל 16.

(*) – אקטיבציית squash הינה פעולה לא לינארית שהופכת וקטור Sj להפוך לוקטור Vj בגודל שבין 0 ל 1:

squash function

אם כך זו רשת CNN רגילה… איפה פה הקפסולות ?

“חבויות” פה שתי שכבות קפסולות:

האחת נקראת Primary Caps ומכילה 6*6*32=1152 קפסולות שכל אחת מחזירה וקטור $u_{i}$ ממימד 8 ובנוסף מחזירה 10 וקטורי פרדיקציה $\widehat{u}_{j|i}$ שהינם המוצא של בלוק DigitCaps. j=1..10, i=1..1152)).

וקטורי המוצא של קפסולות אלו מסודרות כ-32 לוחות כל אחד בגודל 6×6, מיקום הקפסולות בלוח ה- 6×6 פורפורציונלי למיקום (x,y) בתמונה המקורית. (ז”א למשל קפסולה במיקום שמאלי עליון בלוח 6×6 מייצג את המידע בתמונה שנמצא בפינה שמאלית עליונה)

השניה נקראת DigitCaps מכילה 10 קפסולות שכל אחת מחזירה וקטור $v_{j}$ ממימד 16 (מחושבים באמצעות אלגוריתם Routing). קפסולות אלו לא מחזירות וקטורי פרדיקציה כי אין שכבה שלישית במימוש זה. (התרשים לא מראה את ה dynamic routing על אף שהינו חלק מהרשת)

מה שקצת מבלבל פה זה שמשתתפים פה באימון משתנים נוספים שכדאי שנשים לב אליהם:

כל אחד מהוקטורים $v_{j}$ יש לסמן כ $v_{j}^{r}$ (עם מציין לאינדקס האיטרציה) כי למעשה וקטורי r+1 מחושבים על בסיס וקטורי r.

אז מה בדיוק מאמנים פה ? מהי פונקציית ה Loss ?

פונקציית ה Loss מורכבת ממרכיב ה Margin Loss ומרכיב ה Reconstruction Loss.

מרכיב ה Margin Loss מבוסס על עשרת וקטורי המוצא $v_{j}$ של שכבת הקפסולות השניה (DigitCaps) .

ה- Margin Loss הינו סכום עבור k=0..9 של:

capsule loss function

כאשר Tk=1 אם ורק אם התמונה שהוזנה מכילה ספרה k, והפרמטרים +-m הינם ספים 0.1\0.9 בהתאמה, ו λ=0.5. (ערכים מומלצים לפי המאמר).

משמעות Loss זה בפשטות הינו תתגמל אם Vk מצביעה על הספרה של התמונה שהוזנה ותעניש אם לא.

כמו כן ישנו את מרכיב ה Reconstrucion Loss לו נותנים משקל נמוך והוא למעשה הפרש הריבועים בין התמונה המקורית לבין תמונה משוחזרת.

התמונה המשוחזרת נבנית באמצעות Decoder המורכב משלושה שכבות Fully Connceted שמקבלות את מוצא ה DigitCaps.

מרכיב ה- Reconstruction Loss אינו חובה וכשהוסיפו אותו אכן שיפר תוצאות.

קצת על הקוד

בקישור זה למשל תוכלו למצוא מימוש מלא ב TensorFlow:

https://github.com/naturomics/CapsNet-Tensorflow

הדבר הייחודי ששווה להזכיר שב Dynamic Routing יש לולאה בה כל המשתנים הם חלק מהאימון (ז”א ה Back-Propogation מעדכן אותם) הוא די מבלבל ולא סטנדרטי.

כך למשל ניתן לממש לולאה של טנזורים: (בקישור המימוש קצת שונה)

def condition(input, counter):
return tf.less(counter, 100)

def loop_body(input, counter):
output = tf.add(input, tf.square(counter))
return output, tf.add(counter, 1)

with tf.name_scope(“compute_sum_of_squares”):
counter = tf.constant(1)
sum_of_squares = tf.constant(0)
result = tf.while_loop(condition, loop_body, [sum_of_squares, counter])

with tf.Session() as sess:
print(sess.run(result))

זהו להפעם… אשמח לשאלות ודיונים בנושא!

May

2018

הרעיון מאחורי רשת הקפסולות

מיועד ל- מתחילים (כתבה קצת טכנית)

נכתב על ידי תמיר נווה

תסכימו שזה מעורר סקרנות לשמוע את הינטון שנחשב לאחד האושיות של הלמידה העמוקה נותן הרצאה ב MIT ששמה “מה הבעיה ברשתות קונבולוציה ?”

רקע

זיהוי אובייקטים בתמונות זו משימה שעד 2012 נחשבה מאוד קשה ולאחר מהפיכת הלמידה העמוקה נחשבה להרבה יותר פתירה (תלוי כמובן מה לזהות ובאילו תנאים). הבעיה נחשבת כקשה (עבור אלגוריתם) על אף שלבן אנוש נחשבת כקלה, כי כבני אדם שכבר מנוסים בלזהות ולתמלל מה אנו רואים כבר שכחנו שלמשל תמונה של דג יכולה להיות במגוון ואריאציות, מגוון סוגי דגים, זוויות הסתכלות (שמשנות לגמרי את תוכן התמונה), מגוון אפשרויות לתאורה וצל. את כל אלו כבר למדנו לסנן ולדעת שדג בהיטל על כשזרקור מכוון אליו זה אותו האובייקט כמו דג בהיטל צד בתאורה חשוכה.

לשתי תמונות אלו של דג יש אלמנטים משותפים (סנפירים, קשקשים, רקע של מים,…) ואת אלו למדנו למצוא, ולבדוק אם כל אחד מהם מעיד על אותם מאפיינים של דג שמכיל אותם. ז”א סנפיר מואר בהיטל על עשוי להעיד על דג מואר בהיטל על, קשקשים חשוכים בהיטל צד עשויים להעיד על דג בהיטל צד בתאורה חשוכה. רעיון זה הינו ההשראה לפיתוח רשת הקפסולה.

הינטון דיבר על כך שיש בעיה ברשתות CNN והתייחס לפעולת ה pooling שאומנם עובדת (באופן מקרי) אך מאבדת מידע (מרחבי) חשוב ולכן לא טובה לזיהוי ולכן מציע חלופה.

סיכום המאמר “Transforming Auto-encoders” (2011)

המושג קפסולה מוזכר לראשונה במאמר זה ומודגם עם ארכיטקטורה מאוד פשוטה. (ללא כל קישור לקוד)

כל קפסולה אמורה לטפל באוביקט מסוים (מתוך התמונה הגדולה), לקודד את המאפיינים שלו ומתוכם לשחזר את האוביקט לפי אותם המאפיינים, קצת כמו פעולת ה Rendering בגרפיקה ממוחשבת. למשל נתונים אוביקט כסא ומטריצת טרנספורמציה שיודעת איך לסובב אותו במרחב כדי להציג אותו באופן נכון בסצנה של משרד. פלט של כל קפסולה הינו וקטור שגודלו מציין את ההסתברות לקיומו בתמונה המלאה וכיוונו מציין את המאפיינים שלו, ובתוך כל קפסולה יש כפל במטריצת טרנספורמציה. לטענת הינטון זיהוי במוח האנושי הוא פעולה ההפוכה מ Rendering וקרא לזה Inverse Graphics. ז”א המוח מפרק את התמונה המלאה לאובייקטים ולמאפייניו של כל אוביקט, וכך מזהה מה רואים בתמונה המלאה. (בתלות בהתאמה בין המאפיינים)

במאמר, מדובר על כך שכדי לזהות תמונה (למשל פנים) יש צורך בקידוד של כל אלמנט בתמונה (אף, פה, עיניים) ובמיקומו היחסי לאוביקט כולו (הפנים). כל קפסולה (אם אומנה כיאות) תפקידה לזהות אלמנט מסוים בתמונה ואת המאפיינים היחסיים שלו ביחס לאוביקט. למשל אם יזיזו או ישנו רק אלמנט אחד (נניח האף), הקפסולה לא תשנה את ערכה המציין את ההסתברות למופע שלו אלא רק את המאפיינים היחסיים שלו (מיקום יחסי, תאורה יחסית, מנח יחסי,…). אז למשל בזיהוי פנים בתמונה, אם הקפסולות שמזהות עיניים, אף ופה כולן מסכימות בהסתברות גבוהה שהם קיימים בתמונה ואם ניתן להסיק מכל אחד מהמאפיינים שלהן שגבולות הפנים הם באזור זהה (למשל קונטור הפנים הוא כזה שהאף במרכז, העיניים מעלה והפה מטה) אזי בהסתברות גבוהה שיש פנים בתמונה.

רשת רגילה שמקבלת תמונה עם שני עיניים ואף במיקומים אקראיים עשויה להחליט שזו תמונת פנים, רשת קפסולות כנראה תחליט שזו תמונת פנים רק אם האף מתחת לאמצע הקו המחבר בין העיניים.

הרעיון של הקפסולות פותח בהתחלה ברשת שנקראת .Transforming Auto-encoders רשת זו “מאלצת” את המשתנים הפנימיים שלה ללמוד לזהות חלקים בתמונה ואת מיקומם היחסי.

באופן כללי Auto-encoder זו רשת שמאמנים אותה לקבל תמונה, ולהחזיר את אותה התמונה אבל בשכבות הביניים שלה יש מעט משתנים כך שאין לרשת אפשרות להוציא בדיוק את מה שקיבלה Identity (כי זה הרי לא חוכמה), היא נאלצת לקודד את התמונה הנקלטת למעט משתנים ולשחזר את התמונה כולה מתוכם.

ב- Transforming Auto-encoders מאלצים את הרשת לקודד את התמונה לפי חלקים שלה ומיקומם היחסי.

תודה ל Transforming Auto-encoders

בתרשים זה ניתן לראות הדגמה פשוטה של הרעיון רק על הזזה. בתרשים יש שלוש קפסולות שכל אחת מהם מקבלת תמונת קלט (הסיפרה 2) והיא מורכבת משכבת מקודד Encoder (העיגולים האדומים) ומשכבת מפענח Decoder (העיגולים הירוקים). מאמנים את הרשת הזו כך שתקבל את התמונה ותחזיר אותה מוסטת ב ∆y,∆x. בנוסף לקלט התמונה גם מזינים את ההסטה ז”א את זוג הערכים ∆y,∆x. כל קפסולה מכילה רק שלושה משתנים פנימיים x,y,p שמשמעותם מיקום האלמנט (או מיקום האוביקט כולו בתמונה אם זה האלמנט שלו) וההסתברות לקיומו בתמונה. תמונת הפלט הסופית משלושת הקפסולות משקללות פלט של כל קפסולה לפי ההסתברות p שלה.

כותבי המאמר לקחו רשת מבנה כזה אך עשיר יותר (30 קפסולות, 10 נוירונים במקודד ו 20 נוירונים במפענח) ואימנו אותה על מאגר MNIST כאשר מבצעים בכל פעם הסטה אקראית של התמונה אופקית או אנכית עד כשני פיקסלים בכל פעם. הם קיבלו שהמשתנים הפנימיים x,y במוצא ה encoder תואמים להסטה של התמונה ∆y,∆x מה שאומר שכל קפסולה למדה לזהות אלמנט מסויים בתמונה במיקום מסוים. וכשישנה הסכמה על המיקומים של האלמנטים המרכיבים ספרה מסוימת אזי זו אכן הספרה המסוימת ולא אחרת.

איך התקדם מאז ?

ארכיטקטורת הקפסולות חזרה לכותרות ב 2017 במאמר של הינטון וחבריו האחרים בו הם מציעים ארכיטקטורת קפסולות יותר מורכבת ויותר חשוב מזה מציגים שיטה איך לאמן קפסולות (Dynamic Routing). ייתכן ואכתוב על כך מאמר נוסף בהמשך (תלוי בביקוש שלכם הקוראים…) אך מה שחשוב להבין זה את התוצאות שלהם. כשהשוו ביצועים של CNN קלאסי לזיהוי ספרות ב MNIST הדורש אותם משאבי חישוב בערך כמו רשת הקפסולות שלהם, ניצחה רשת הקפסולות בהסתברות הזיהוי (הגיעה ל-0.25% שגיאה), מה גם שדרשה פחות זיכרון. (8.2M פרמטרים לעומת 35.4M פרמטרים ב CNN אליו הושוו התוצאות)

המחקר על הגישה עדיין בראשיתה ועוד לא ברור באופן מוחלט שהיא תמיד עדיפה באופן כללי (למשל על מאגרי תמונות יותר גדולים ומאתגרים מ- MNIST), במאמר יש דיון בין השאר על אחד החסרונות של השיטה שנקרא crowding שזה קושי בזיהוי אוביקטים זהים וקרובים מה שגם קורה בזיהוי אנושי. ללא ספק מבחינה רעיונית יש כאן התקדמות ששווה להכיר!