הפוסט פורסם לראשונה בבלוג המחקר של איציק בן שבת ומובא כאן בתרגום לעברית.
הקדמה
שיטות למידה עמוקה ורשתות נוירונים הפועלות על תמונות דו מימדיות נחקרו רבות בשנים האחרונות. ההצלחה המסחררת שלהן במשימת ה”סיווג” נובעת מכמה גורמים עיקריים :
- רשתות קונבולוציה
- נתונים – מאגרי תמונות עצומים הפכו לזמינים ופתוחים לכולם.
- כוח חישוב
הזמינות של מידע תלת מימדי מתחילה לגדול בקצב מסחרר. בין אם מדובר בחלקי תיב”ם (CAD תכנון וייצור באמצעות מחשב) שתוכננו על ידי אדם או על מידע שנסרק על ידי חיישן LiDAR או מצלמת עומק (RGBD) – ענני נקודות נמצאים בכל מקום !
לכן, אחד הצעדים הבאים המתבקשים במחקר הוא להבין איך אנחנו יכולים לקחת את הכלים המדהימים שפותחו בתחום של למידה עמוקה, שעובדים כל כך טוב על תמונות, ולהרחיב אותם לתלת מימד ?
אתגרים
מסתבר שהמעבר לא כל כך פשוט. אחלק את האתגרים לשני סוגים עיקריים : אתגרים “חדשים” שקשורים לתהליך הלמידה ואתגרים ” ישנים” שקשורים לאופי המידע השונה.
אתגרי רשתות הנוירונים:
- מידע לא סדור (אין סריג): ענני נקודות הם למעשה אוסף של קואורדינטות XYZ מרחביות. לכן, אין מבנה סריג שמאפשר להשתמש בכח של רשתות קונבולוציה (שיתוף משקלים של פילטרים אינוואריאנטים להזזה)
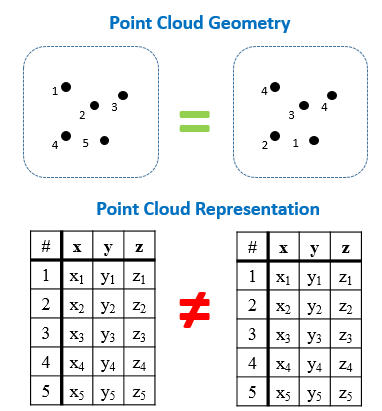
- אינוואריאנטיות לפרמוטציות: ענן נקודות הוא למעשה רשימה ארוכה של נקודות (מטריצה בגודל nx3, כאשר n הוא מספר הנקודות). גיאומטרית, לסדר הנקודות אין משמעות אבל לסדר הופעתן במטריצה יש משמעות, כלומר, ניתן לייצג את אותו ענן על ידי מספר רב של מטריצות שונות. (ראה תמונה מטה להמחשה)
- מספר נקודות משתנה: בתמונת, מספר הפיקסלים ידוע מראש וקבוע כתלות במצלמה. מספר הנקודות, לעומת זאת, יכול להשתנות בצורה קיצונית כתלות בחיישן ובתנאי הסביבה.
אתגרי אופי הנתונים:
- מידע חסר: העצמים הסרוקים בדרך כלל מוסתרים בחלקם ולכן חלק מהמידע חסר
- רעש: כל החיישנים רועשים. יש מספר סוגים של רעש הכוללים פרטורבציות (לכל נקודה סרוקה יש הסתברות מסויימת להמצא סביב הנקודה האמיתית בתוך ספרה בעלת רדיוס בגודל מסויים) ונקודות חריגות outliers (נקודה המופיעה במיקום אקראי במרחב).
- סיבובים: לאותו האוביקט יהיה ענן נקודות שונה אם הוא באוריינטציה שונה אפילו אם נסרקו בו אותם הנקודות, למשל ענני נקודות של מכונית שפונה ימינה או שמאלה.
- ההרחבה ה”מיידית” להפעלת למידה עמוקה על ענני נקודות היא להעביר את הענן לייצוג נפחי (ווקסלים), ז”א איפה שאין דגימה שמים אפס ואיפה שיש דגימה שמים אחד. כך, נוכל לאמן רשת קונבולוציה עם פילטרים תלת מימדיים ולהימנע מכל האתגרים שקשורים לרשתות נוירונים על ענני נקודות (סריג הווקסלים פותר את בעיית המידע הלא סדור, ההמרה לווקסלים פותרת את בעיית הפרמוטציות ומספר הווקסלים קבוע ומוגדר מראש). אולם, לגישה זו יש חסרונות משמעותיים. ייצוג נפחי הופך להיות גדול מאד, מהר מאד. למשל, עבור תמונה אופיינית בגודל 256×256= 65536 פיקסלים נוסיף את מימד הנפח ונקבל 256X256X256=16777216 ווקסלים. זה הרבה מאד מידע (אפילו לכרטיסים גראפיים חדשים שכמות הזיכרון בהם גדל מאד בשנים האחרונות). מלבד גודל הזיכרון לאחסון, המשמעות של נתונים רבים כל כך היא זמן עיבוד איטי מאד. לכן, בהרבה מקרים “מתפשרים” ולוקחים רזולוציה נפחית נמוכה יותר (בחלק מהשיטות 64X64X64) שעולה לנו במחיר של שגיאת קוואנטיזציה.
אזזזזזזזזזזזזזזזזזזז, הפיתרון הרצוי לעיבוד ענני נקודות באמצעות למידה עמוקה צריך לעבוד בצורה ישירה על הנקודות.
הדטסט
כמו בכל בעיה בתחום הראייה הממוחשבת, אם ברצוננו להוכיח ששיטה עובדת, צריך להראות את זה על אמות מידה (Benchmark) מקובל בתחום.
אני אתמקד ב ModelNet40 מבית היוצר של פרינסטון. הוא מכיל 12311 מודלי תיבם עם 40 קטגוריות של אובייקטים (מטוסים, שולחנות, צמחים וכ’) ומיוצג על ידי רשתות משולשים Triangle mesh (קירוב של משטח חלק על ידי אוסף של מישורים הנפוץ בעולם הגראפיקה). מחלקים את הסט ל9843 מודלים לאימון ו 0135 לבדיקה. ביצעתי קצת ויזואליזציות של הדטסט עם קוד הגיטהאב שפותח עבור שיטת PointNet (תודה לצ’ארלס)

סקר ספרות
בפוסט הזה אסקור 3 שיטות שמבצעות למידה ישירות על ענני נקודות.
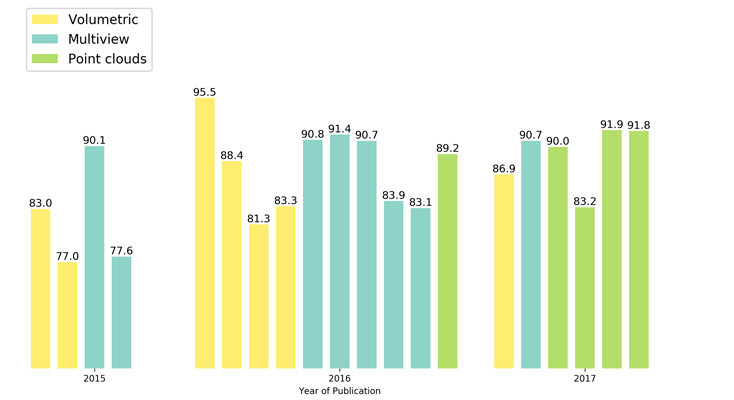
אבל שניה לפני זה אני רוצה להראות גרף עמודות המסכם מספר שיטות עדכניות (נכון לתחילת 2018) ובאיזה סוג נתונים כל אחת משתמשת. אפשר לראות שב-2015 רוב השיטות עבדו על תמונות דו מימדיות של אובייקט תלת מימדי שצולמו ממספר נקודות מבט שונות (Multi-View), ב-2016 מספר גדול יותר של שיטות השתמשו בייצוג נפחי עם PointNet החלוצה שהתחילה לעבוד על ענני נקודות ושב-2017 חלה עליה בשיטות המנסות לעבוד ישירות על ענני נקודות.
PointNet – CVPR 2017
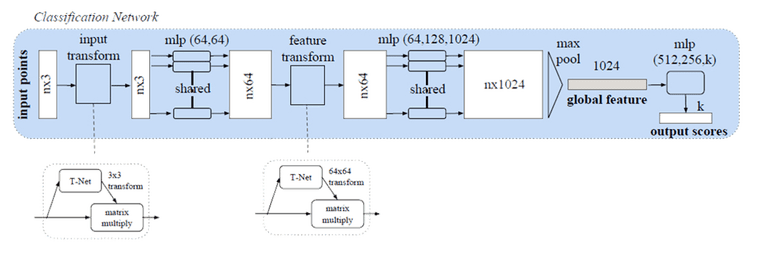
המאמר פורסם ב arXiv בסוף 2016 ומיד משך תשומת לב רבה. הגישה לפיתרון פשוטה מאד והם הציגו הסברים תיאורטיים למה היא עובדת טוב. הם אימנו פרספטרון רק שכבתי (MLP) על כל נקודה בנפרד (עם משקלים משותפים בין הנקודות השונות). כל נקודה “הוטלה” למרחב ממימד 1024. אחר כך פתרו את בעיית סדר הנקודות על ידי הפעלת פונקציה סימטרית (מקסימום) על כל הנקודות. התוצאה היא ווקטור באורך 1024 שניתן להתייחס אליו כמתאר (פיצ’ר) גלובאלי לכל ענן נקודות. את המתאר הזה הם הזינו למסווג לא לינארי (רשת fully connected). הם גם פתרו את בעיית הרוטציה על ידי הוספת תת רשת קטנה (T-net). תת הרשת הזו לומדת לשערך מטריצת טרנספורמציה על הנקודות (3×3) ועל מתארים ממימד ביניים (64×64). לקרוא לרשת זו “תת רשת” זה קצת מטעה כי כי גודלה קרוב לגודל הרשת הראשית. בנוסף, בגלל העלייה המשמעותית במספר הפרמטרים הם הוסיפו לפונקציית המחיר אילוץ שגורם למטריצת הטרנספורמציה לשאוף לארותוגונליות.
הם גם עשו סגמנטציה לחלקים עם רשת דומה מאד.
והם גם עשו סגמנטציה סמנטית על סצנות.
והם גם עשו שיערוך נורמאלים.
עבודה מדהימה! אני מאד ממליץ לקרוא (או אפילו לצפות בסרטון המצגת)
התוצאה שלהם עם ModelNet40 היתה 89.2% דיוק.
Cite: Charles R. Qi, Hao Su, Kaichun Mo, and Leonidas J. Guibas. Pointnet: Deep learning on point sets for 3d classication and segmentation. In The IEEE Conference on Computer Vision and Pattern Recognition (CVPR), July 2017.
הקוד זמין בגיטהאב: PointNet code
Deep Sets – NIPS2017 / ICLR2017
החבר’ה האלה מ CMU פרסמו את העבודה הזאת מספר שבועות לפני PointNet. הרעיון הכללי מאד דומה (לא לוקח צד בויכוח מי חשב עליו קודם). המיקוד של המאמר הזה הוא ייצור שכבה שמקבילה לקונבולוציה שפועלת על סטים (סט של נקודות במקרה שלנו) שנקראת שכבת ה”שקילות לפרמוטציות” ( permutation equivariance = PE) שזמן החישוב שלה הוא לינארי ביחס לגודל הסט. הם טוענים ששכבת ה PE היא הצורה הטובה לשיתוף משקלים למטרה זו. הניסויים מראים ביצועים משופרים לסיווג ענני נקודות (90%).
הם גם עושים חיזוי לסכום ספרות MNIST.
הם גם עושים זיהוי אנומליות בסטים.
עבודה מאד מעניינת, מאד ממליץ לקרוא למי שיותר מוכוון תיאוריות בשיטות למידה.
Cite: Ravanbakhsh, Siamak, Jeff Schneider, and Barnabas Poczos. “Deep learning with sets and point clouds.” arXiv preprint arXiv:1611.04500 (2016).
Zaheer, M., Kottur, S., Ravanbakhsh, S., Poczos, B., Salakhutdinov, R. R., & Smola, A. J. (2017). Deep sets. In Advances in Neural Information Processing Systems (pp. 3394-3404).
הקוד זמין בגיטהאב: Deep sets code
Pointnet++ – NIPS 2017
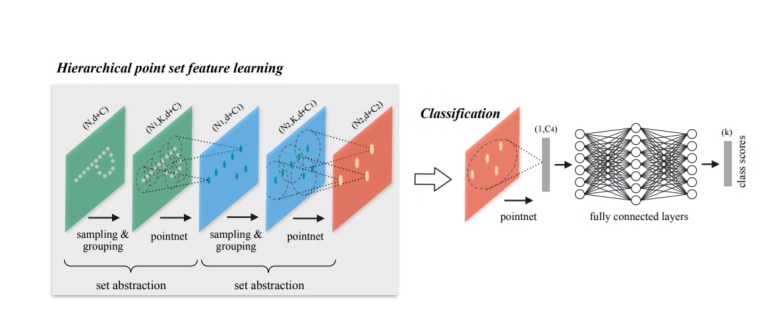
כשקראתי לראשונה את PointNet היה דבר אחד שמאד הטריד אותי – למה הם לא משתמשים בשכנויות מקומיות ? אז, אני מניח שזה הטריד גם אותם כי לא עבר זמן רב והם הוציאו לאויר העולם את PointNet++. זאת למעשה גירסה הירארכית של המקור. לכל שכבה יש שלושה תתי שלבים : דגימה, איסוף ופינטנוט (pointnetting). בשלב הראשון, הם בוחרים מרכזים, בשלב השני הם יוצרים אוסף של תתי עננים מקומיים מהשכנים של כל מרכז (ברדיוס נתון). לאחר מכן הם מזינים אותם לפוינטנט ומקבלים ייצוג מסדר גבוהה של תת הקבוצה. לאחר מכן הם חוזרים על התהלים (דוגמים מרכזים, מוצאים שכנים, ומריצים פוינטנט על הייצוג ממימד גבוהה יותר כדי לקבל ייצוג ממימד גבוהה עוד יותר). הם ביצעו שימוש ב3 שכבות כאלה (3 רמות הירארכיה). הם גם בחנו מספר שיטות איסוף על מנת להתגבר על בעיות הקשורות לצפיפות ענן הנקודות (בעיות שקיימות כשמשתמשים בכל חיישן תלת מימדי = נקודות צפופות קרוב לחיישן ודלילות רחוק מהחיישן). הם השיגו שיפור על המקור עם דיוק של 90.7% על ModelNet40 (שיפור גבוה יותר התקבל כשהשתמשו בווקטורי הנורמל לכל נקודה).
Cite: Charles R Qi, Li Yi, Hao Su, and Leonidas J Guibas. Pointnet++: Deep hierarchical feature learning on point sets in a metric space. arXiv preprint arXiv:1706.02413, 2017
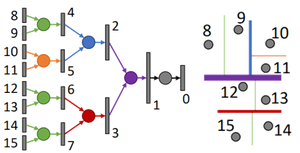
Kd-Network – ICCV 2017
המאמר הזה משתמש במבנה הנתונים הידוע Kd-tree כדי ליצור סדר בענן הנקודות. לאחר הכנסת הענן למבנה, הם לומדים משקלים לכל צומת בעץ (שמייצגת חלוקה של המרחב בציר מסויים). המשקלים משותפים לכל ציר בכל רמה בודדת בעץ (כל הירוקים בתמונה למטה יש משקלים משותפים כי כולם מחלקים את המרחב בציר x). הם בחנו תת חלוקה ראנדומאלית ודטרמיניסטית של המרחב ומדווחים שהגישה הראנדומלית עובדת טוב יותר. הם מדווחים גם על מספר חסרונות. הגישה רגישה לסיבוב (כי רוטציה משנה את מבנה העץ) ורעש (במידה והוא משנה את מבנה העץ). אני מצאתי חיסרון נוסף – מספר הנקודות: לכל קלט בעל מספר נקודות שונה צריך לבצע דגימה מחדש למספר הנקודות שעליו הרשת אומנה או לחלופין לאמן רשת חדשה שתתאים למספר הנקודות הנתון.
הם מדווחים דיוק של 90.6% עבור 1024 נקודות בענן (עץ בעומק 10) ודיוק של 91.8 עבור ~32K נקודות (עץ בעומק 15) על ModelNet40.
למרות החסרונות, אני מוצא את הגישה לפיתרון מאוד מעניינת. בנוסף, נראה שיש עוד עבודה לעשות (למשל לנסות מבני עץ אחרים כפי שהם מציעים במאמר).
הם גם עשו סגמנטציה לחלקים ו Shape Retrieval.
Cite: Roman Klokov and Victor Lempitsky. Escape from cells: Deep kd-networks for the recognition of 3d point cloud models. arXiv preprint arXiv:1704.01222, 2017.
סיכום
בקהילת הvision, התוצאות הסופיות מאד חשובות ולכן ריכזתי אותן כאן בטבלה:

אפשר לראות שהתוצאות יחסית קרובות אחת לשניה ויש הרבה השפעות של פרמטרים וגורמים שונים. לכן, אני מוצא עניין רב בהבנה של אופן הפעולה של כל שיטה. PointNet ואחותה הגדולה PointNet++ עושים שימוש בפונקציות סימטריות כדי לפתור את בעיית הסדר בעוד שKd-Network עושה שימוש בעץ Kd. העץ גם פתר את בעיית הסדר בעוד שבפוינטים הפרספטרון אומן על כל נקודה בנפרד.
אני פיתחתי שיטה משלי (יחד עם המנחים שלי בטכניון כמובן) תוצרת כחול לבן לפתרון הבעיה הנקראת 3DmFV-Net. ארחיב עליה בפוסט הבא. למי שאין סבלנות מוזמן לקרוא את המאמר, להיכנס לפוסט המסביר על השיטה בבלוג שלי, לצפות בסרטון היוטיוב בנושא ולהשתמש בקוד. השיטה פורסמה בכנס 2018 IROS ובעיתון Robotics and Aautomation Letters.

