מהם גרפים והיכן הם מופיעים
כיצד הייתם מתארים את העולם שמסביבכם באופן שמאפשר לראות את הן את האובייקטים הנמצאים בו והן את היחסים ביניהם? איך הייתם שומרים על כל המידע הזה בצורה שמאפשרת ניתוח מהיר ומועיל?
בדיוק לצורך זה הומצאו גרפים. מבחינה אינטואיטיבית, גרפים הינם אוסף של אובייקטים שקשורים אחד לשני. מבחינה מתמטית, גרפים הינם זוג סדור כאשר הוא אוסף קודקודים (האובייקטים), ו- הוא אוסף הקשתות (הקשרים) ביניהם.
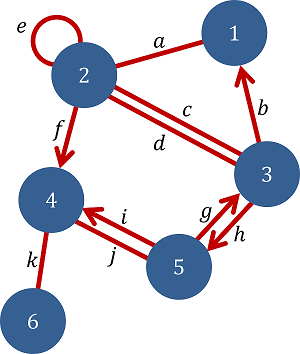
תודה ל https://commons.wikimedia.org/wiki/User:R%C3%B6mert
בעוד אנו יכולים לייצג הרבה מהמידע בו אנו עוסקים באופן סדרתי (לדוגמה, תמונות ניתן לייצג ע”י מטריצת פיקסלים), גרפים הם מבנים מורכבים הרבה יותר מעצם הגדרתם. בעוד בתמונה פיקסל כלשהו קרוב רק למספר קטן של פיקסלים (ספציפית, אלו שסובבים אותו בתמונה), בגרף קודקודים יכולים להיות “קרובים” אחד לשני (כלומר, קיימת ביניהם קשת) גם אם הם נמצאים בקצוות שונים של הגרף. מצד אחד, מורכבות זו מאפשרת לנו לתאר מידע מגוון הרבה יותר מאשר שתמונה יכולה לייצג. ניתן למצוא מידע רב שמיוצג בעזרת גרפים, החל מרשת ציטוטים בין מאמרים, דרך רשת קישורים בין אתרי אינטרנט וכלה במערכת כבישים ותחבורה.
מצד שני, בדיוק בגלל מורכבות זו, קשה הרבה יותר להשתמש בכלים הסטנדרטיים של למידת מכונה על גרפים. אנחנו לא יכולים לקחת גרף ופשוט “לזרוק” אותו על רשת נוירונים ולצפות שהיא תלמד בצורה מוצלחת. רשתות נוירונים, על שלל צורותיהן, נועדו ללמוד מידע סדרתי מסוג כזה או אחר. על מנת להצליח ללמוד מתוך גרפים, אנחנו צריכים ללמוד מידע מרחבי.
למידה עקיפה
מהו מידע מרחבי? מידע מרחבי הוא מידע שיודע לייצג את הקשר בין מספר רב של אובייקטים ומייצג את האופן בו האובייקטים קשורים אחד לשני. דוגמה למידע מסוג זה ניתן לראות במדדי מרכזיות, שנובעים מהתיאוריה של תורת הרשתות. מדדי מרכזיות מאפשרים לכמת את החשיבות של כל קודקוד ברשת באמצעות סדרת נוסחות מוגדרות מראש. כך לדוגמה, אנו יכולים לתת ניקוד גבוה יותר לקדקודים שמרכזיים יותר ברשת. דוגמה פשוטה למרכזיות היא לתת לכל קודקוד ציון לפי כמות הפעמים שהוא נמצא במסלול הקצר ביותר בין שתי קודקודים אחרים. ניתן לחשוב על דוגמה של מערכת כבישים. אם צומת כלשהי נמצאת במסלול הקצר ביותר של רבים מהמסלולים אותם ניתן לעבור, צומת זו תהיה צומת מרכזית יותר במובן כלשהו. לחילופין, אתר אינטרנט שאליו יש קישורים מאתרים רבים אחרים הוא אתר מרכזי במובן אחר. כל אחד מהמובנים האלו שקול לאלגוריתם מרכזיות שונה.
רשימה גדולה של מדדי מרכזיות ניתן למצוא בספריה Networkx, ספרית פייטון שמאפשרת בניה וניתוח של גרפים.
ניתוח של מידע מרחבי, כדוגמת מרכזיות, מאפשר לנו להסיק מסקנות על גרפים, בין היתר תוך שימוש בלמידת מכונה. ע”י חישוב מידע מרחבי מסוגים שונים (מידע כזה באופן כללי נקרא feature או “מאפיין”) אנו יכולים לבנות מטריצות של מידע שמצד אחד מכיל את המידע המרחבי שרצינו ומצד שני בנויות באופן מסודר מספיק בשביל שמכונה תוכל ללמוד מתוכו. כך לדוגמה נוכל לבנות “וקטור features” לכל קודקוד בגרף ולאחד את כולם למטריצה שמייצגת את הגרף כולו. למידה מתוך וקטורים כאלו מאפשרת פעולות רבות בשיעורי הצלחה לא רעים, לדוגמה סיווג של קודקודים לפי סוג, גילוי של קשרים שחסרים ברשת וכן הלאה.
למידה מתוך מבנה הגרף
למידה מתוך מאפיינים שבנויים ידנית, למרות הצלחתה היחסית, לא יכולה להיות השיטה הטובה ביותר. דוגמה לתהליך מסוג זה אנחנו יכולים לראות בהתפתחות הלמידה העמוקה על תמונות. בעבר הרחוק (בערך עד 2012) מעבר לשימוש ברשתות נוירונים רגילות (Feed-Forward Networks), הדרך היחידה לשפר למידה על תמונות הייתה ע”י שינויים ידניים שנעשו לתמונות, בין אם שינויים לתמונות שהוכנסו ללמידה ובין אם פיצ’רים שחושבו על התמונות והוכנסו לרשתות בנוסף לתמונות עצמן. קפיצת המדרגה הגדולה בלמידה על תמונות הייתה כאשר הכניסו למשחק רשתות שיודעות גם ללמוד את הפיצ’רים האופטימליים עבור הנתונים, רשתות שכיום ידועות בשם רשתות קונבולוציה.
בואו ניזכר מה עושות רשתות קונבולוציה. בכל שלב רשת הקונבולוציה מפעילה אוסף של “פילטרים” שמטרתם למצוא תבניות דומות בכל התמונה. ככל שישנן יותר שכבות קונבולוציה כך התבניות שנלמדות נהיות יותר ויותר מורכבות. נרצה לעשות אותו דבר עבור גרפים.

https://arxiv.org/pdf/1311.2901.pdf
הבעיה העיקרית בגישה זו, כפי שכבר ראינו, היא שאנחנו לא יכולים להגדיר “סביבה” של קודקוד עליה אנו יכולים לבצע את הקונבולוציה. במקום זאת, עלינו לעבוד על מטריצת השכנויות של הגרף.
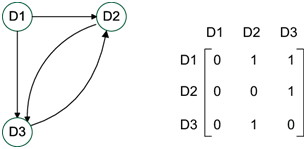
מטריצת השכנויות של גרף הינה מטריצה בה אם ישנה קשת בין קודקודים ו- אז בשורה ה- בעמודה ה- נכניס את משקל הקשת ביניהם (או 1 אם הגרף שלנו לא ממושקל).
למעשה, ניתן לחשוב על כל שורה/ עמודה במטריצה זו כמייצגים את “הסביבה” של הקודקוד הרלוונטי. נרצה לנצל את עובדה זו. אם נחשוב על כל שורה באופן זה, המטרה שלנו כעת היא לזהות “תבניות” בין שורות שונות. כיצד ניתן לעשות זאת?
קונבולוציות על גרפים Graph Convolutional Network
בשנת 2017 הוציאו שניים מהמוחות המבריקים ביותר בתחום למידת המכונה על גרפים, תומס קיפף ומקס וולינג, את אחד מהמאמרים בעלי ההשפעה הרחבה ביותר בתחום, Semi-Supervised Classification with Graph Convolutional Networks. במאמר זה הציגו לראשונה השניים את מה שהם כינו “רשתות קונבולוציה על גרפים”, רשתות שיכולות ללמוד תבניות בין קודקודים שונים באופן דומה לקונבולוציות על תמונות. השניים הציעו את המבנה הבא לשכבה אחת ברשת שלהם:


במקרה זה פשוט להבין מה הצורה ש-W תקבל. מכיוון שכפל מטריצות מוגדר ככפל שורה מהמטריצה השמאלית בעמודה מהמטריצה הימנית, נקבל שכל עמודה במטריצת המשקלים מוכפלת בכל שורה במטריצת השכנויות. אם כן, קיבלנו כי כל עמודה במטריצת המשקלים למעשה עוברת על כל “הסביבה” של הקודקודים, באופן זהה לחלוטין לקונבולוציות על תמונות. התוצאה של אימון רשת כזו הינה שכל עמודה במטריצה תהווה מסנן לסוג מסויים של קודקודים.
כעת נחזור למקרה הכללי. הדבר היחיד שנוסף הוא התוצאה של השכבה הקודמת. אבל בהקבלה לקונבולוציות על תמונות, כעת אנו יכולים לראות שהחצי הראשון של הביטוי
![]()
למעשה מחשב עבורנו את אוסף הפילטרים הפשוטים יותר, מה שמאפשר לנו לחשב בשכבה זו צירופים של פילטרים אלו על מנת ליצור מבנים מורכבים יותר.
במבט על, כל המבנה הנ”ל מאפשר לנו לתת לרשת שלנו ללמוד את הפיצ’רים האופטימליים עבור הבעיה שלנו במקום שנצטרך לבנות אותם בעצמנו, כל זאת ע”י חישוב של פילטרים שמזהים מבנים יותר ויותר מורכבים ככל שמספר השכבות עולה.
תוצאות
מעבר לתאוריה היפה, למבנה זה גם תוצאות מרשימות במיוחד.
במאמר, מציגים את רשת בעל שתי שכבות שמצליחה ללמוד את החלוקה שמוצגת בצד ימין מתוך 5% מהתוויות בלבד (על Cora dataset שהינו מאגר נתונים במבנה גרף של מאמרים מדעיים וקשרי ציטוטים ביניהם). למעשה, הרשת הצליחה לזהות קודקודים (ז”א מאמרים מדעיים) דומים והניחה שהם מקבלים סיווג דומה למעט הקודקודים עליהם היה לה מידע.
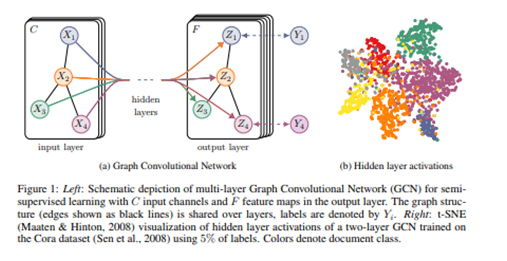
לקוח מ https://arxiv.org/pdf/1609.02907.pdf
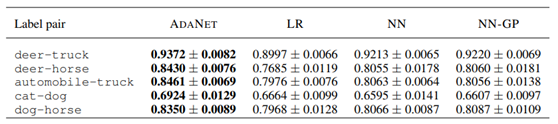
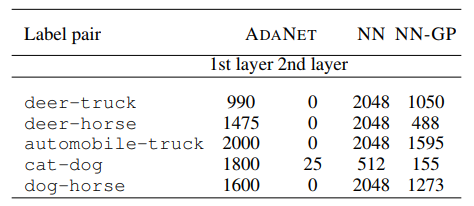
במאמר משווים הכותבים את המאמר שלהם לשש מהשיטות הקיימות לסיווג של קודקודים:

https://arxiv.org/pdf/1609.02907.pdf
כפי שניתן לראות, לפחות עבור הדאטאסטים הסטנדרטים הללו, קונבולוציות על גרפים (Graph Convolutional Networks, GCN) משיגות את התוצאות הטובות ביותר בפער משמעותי.
כמו קונבולוציות על תמונות בשעתן, גם קונבולוציות על גרפים היוו פריצת דרך שהובילו לאינספור כלים חדשים שהיום נמצאים בשימוש. כלים כגון אלו סוללים את הדרך לעבר הבנה טובה יותר של העולם סביבנו וכן נותנים לנו את היכולת לשפר אותו.
קישורים