על דיאגרמת וורונוי, ואיך היית נראה בתור קורי עכביש?

קשה לפספס את הטרנד של רשתות גנרטיביות שחוזות איך היית נראה בתור משהו. בפוסט הבא אני הולכת להראות דרך מגניבה להפוך תמונה לציור דמוי קורי עכביש בשיטה קלאסית המשתמשת בדיאגרמת וורונוי.

אחרי לפני

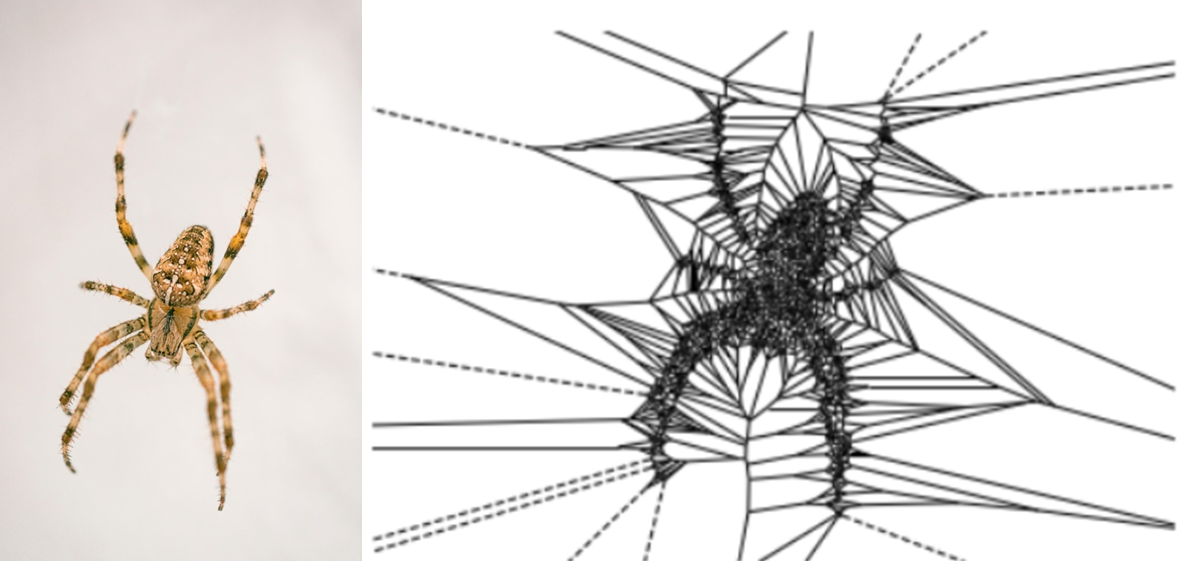
תודה ל Photo by Alexandre Debiève on Unsplash

מהי דיאגרמת וורונוי?

בלונדון של 1854 התפרצות כולרה הרגה 10% מהאוכלוסייה. הרופאים של אותה תקופה חשבו שהמחלה מופצת על ידי “אוויר רע” הנובע מהביוב הפתוח המסריח. אבל לרופא אחד, ג’ון סנואו, האמין שהמשאבה הספציפית שברחוב ברוד היא מקור המחלה.

ג’ון הניח שכל אדם הולך למשאבת מים הקרובה ביותר, ולכן לקח מפה, סימן בנקודות את משאבות מים, ותחם את האזור בו המשאבה ברחוב רוד הייתה מקור המים הקרוב ביותר.

אורכי המלבנים השחורים מייצגים את כמות התמותה בכל כתובת, כשהציג ג’ון את הנתונים באופן שכזה הוא למעשה הביא הוכחה ראשונית להשערה שלו שהכולרה מקורה במים.

מי אמר שלא היה DataSciense פעם 🙂

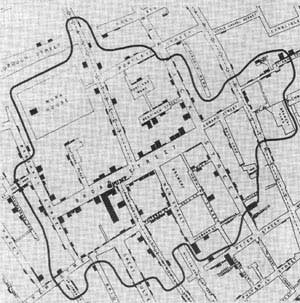
תודה ל – https://plus.maths.org/content/uncovering-cause-cholera

עבור קבוצת אתרים (נקודות) במרחב. דיאגרמת וורונוי היא חלוקה של המרחב לתאים לפי הקרבה לאתרים, תא של אתר הן כל הנקודות בהן האתר הוא האתר הקרוב ביותר.

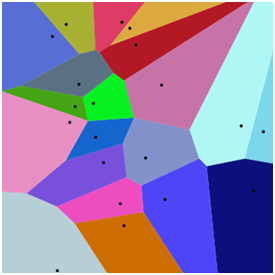
תודה ל – Balu Ertl wikipedia

לחובבי האלגוריתמים – איך מחשבים דיאגרמת וורונוי ?

תרגישו חופשי לדלג על סעיף זה אם מה שמעניין אתכם זה יותר הצד האומנותי\מימושי.

הדרך הכי מיידית (brute force) הינה לחשב לכל נקודה במישור שלנו את המרחקים מכל אחת מהנקודות הנתונות ולבסוף לסווג כל נקודה לפי למי היא הכי קרובה. מימוש זה כמובן איטי מידי.

דרכים נוספות מבוססות על העובדה שלבעיה של מציאת דיאגרמת וורונוי לאוסף נקודות במישור יש בעיה דואלית שנקראת טריאנגולציית (שילוש\תילות) דלאוני שמהותה: חלוקה של הקמור של קבוצת הנקודות למשולשים כך שכל הנקודות בקבוצה הן קודקודים של המשולשים) כך שאף נקודה אינה נמצאת בתור המעגל החוסם אחד מהמשולשים. תכונה זו של השילוש הופכת אותו לאופטימלי, מבחינות מסוימות, משום שהיא מבטיחה שהמשולשים שירכיבו את השילוש יהיו עבים ושמנמנים, ולא ארוכים ודקים.

תודה ל -Hferee

הבעיות דואליות כי אם מחשבים את שילוש דלאוני לאוסף נקודות במישור ואז מעבירים קו בין כל 2 תאים שיש בינהם קשת מקבלים את דיאגרמת וורונוי לאותו אוסף הנקודות.

כיוון שכך, ניתן לחשב את דיאגרמת וורונוי באמצעות אלגוריתמים למציאת טריאנגולציית דלאוני כמו Bowyer–Watson .Bowyer–Watson הוא אלגוריתם אינקרמנטלי. האלגוריתם מתבצע על ידי הוספת נקודה אחת בכל פעם ומעדכן את הטרנגולצייה של תת הקבוצה לאחר כל הוספה. זמן הריצה הממוצע של האלגוריתם הוא $O(n\cdot log\left ( n \right ))$ , אך קיימים מקרים בהם זמן הריצה גדול מ $O(n^{2})$ .

ויש גם אלגוריתמים יעילים למציאת דיאגרמת וורונוי ללא קשר לבעיה הדואלית. למשל בעזרת אלגוריתם שנקרא פורצ’ן (Fortune’s algorithm) ניתן למצוא את דיאגרמת וורונוי של n מרכזים בזמן $O(n\cdot log\left ( n \right ))$ :

By Mnbayazit – https://en.wikipedia.org/wiki/File:Fortunes-algorithm.gif, Public Domain, https://commons.wikimedia.org/w/index.php?curid=32553992

האלגוריתם עובד בצורה של החלקה (sweep), קו אנכי שמתקדם משמאל לימין. האלגוריתם מטפל במרכזים לפי הסדר משמאל לימין ו”מגדיל” את התאים סביב מרכזים שנמצא משמאל לקו. ברגע שתא חסום לגמרי על ידי תאים אחרים, הוא לא גדל יותר. בכל שלב האלגוריתם מתעסק רק עם התאים משמאל לקו שעדיין גדלים, המכונים “קו החוף”. התאים הגדלים מיוצגים כפרבולות הגדלות סביב המרכז שלהם יחד עם התקדמות הקו האנכי. לקריאה נוספת על האלגוריתם.

חומר נוסף על חישוב דיאגרמת וורונוי תוכלו למצוא בקישור הזה והזה.

בכל אופן כפי שתראו בקוד שלי אני משתמשת בפונקציה מוכנה של scipy.

איך זה עוזר לי להפוך לספיידרמן?

בהינתן תמונה (צבעונית) כלשהיא עושים כמה פעולות עיבוד תמונה בסיסיות אותן אסביר מיד ואז מחשבים את דיאגרמת וורונוי. כעת לפרטים:

בוחרים תמונה ובשלב ראשון הופכים אותה לגווני אפור:

Photo by Alexandre Debiève on Unsplash

להלן מימוש בפייתון:

כעת נהפוך את התמונה לשחור לבן, נבחר ערך סף בין 0 ל 255, כל פיקסל שצבעו קטן מערך הסף נצבע שחור, אחרת לבן. שימו לב שעבור תמונות שונות נעדיף לקבוע ערך סף שונה בהתאם לבהירות התמונה.

בתמונות עם אזורים כהים ברקע, עדיף להסיר קודם את הרקע.