בכתבה זו מטרתי להסביר באופן מפורש ומספיק מפורט עד כדי שהקורא החרוץ יידע לממש בעצמו את המאמר “Dynamic Routing between Capsules”. למי שלא מכיר את ההקשר ממליץ לקרוא קודם את הרקע בכתבה הזו: “הרעיון מאחורי רשת הקפסולות” שמסבירה את המאמר המוקדם יותר של הינטון: “Transforming Auto-encoders. ואז את הכתבה הזו: “העמקה לרשת הקפסולות Dynamic Routing Between Capsules – תיאוריה” שמסבירה על התיאוריה שבמאמר.
פרקטיקה
המאמר מציע מימוש ספציפי לרעיון זה על פי ארכיטקטורה שמיועדת לזיהוי ספרות MNIST. אשתמש בסימונים המופיעים במאמר ואסביר את הארכיטקטורה.
נשים לב כי באופן כללי אלגוריתם Routing פועל בין כל שתי שכבות קפסולות סמוכות אך במימוש המוצע הוא פועל רק פעם אחת כי יש סה”כ 2 שכבות של קפסולות.
להלן התרשים של מבנה הרשת במאמר: (חייב להגיד שלקח לי זמן רב להבין ממנו מה באמת קורה באלגוריתם, מקווה שאצליח לחסוך לכם זמן זה…)
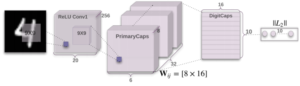
תודה ל Dynamic Routing between Capsules
הסבר על כל בלוק:
-
בלוק הכי שמאלי: הרשת מקבלת תמונה (של ספרה) בגודל 28×28
- בלוק ReLU Conv1: שכבת קונבולוציה שהינה 256 פילטרים בגודל 9×9 ב stride=1 עם אקטיבציית Relu. לכן הטנזור במוצא בגודל 20x20x256.
- בלוק PrimaryCaps: שכבת קונבולוציה שהינה 256 פילטרים בגודל 9×9 ב stride=2 עם אקטיבציית Squash (*). לכן הטנזור במוצא בגודל 6x6x256. אותו טנזור בגודל 6*6*256 אלמנטים מסודר כ 32 טנזורים בגודל 6x6x8. כל אחד מבין ה 32x6x6 וקטורים בגודל 8 כל אחד יסומן
- בלוק DigitCaps: שכבת Fully Connected שממומשת ע”י מטריצה W שהופכת כל אחד מה 6x6x32=1152 וקטורי
לעשרה וקטורי (פרדיקציה)
בגודל 16.
(*) – אקטיבציית squash הינה פעולה לא לינארית שהופכת וקטור Sj להפוך לוקטור Vj בגודל שבין 0 ל 1:
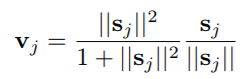
squash function
אם כך זו רשת CNN רגילה… איפה פה הקפסולות ?
“חבויות” פה שתי שכבות קפסולות:
- האחת נקראת Primary Caps ומכילה 6*6*32=1152 קפסולות שכל אחת מחזירה וקטור
ממימד 8 ובנוסף מחזירה 10 וקטורי פרדיקציה
שהינם המוצא של בלוק DigitCaps. j=1..10, i=1..1152)).
וקטורי המוצא של קפסולות אלו מסודרות כ-32 לוחות כל אחד בגודל 6×6, מיקום הקפסולות בלוח ה- 6×6 פורפורציונלי למיקום (x,y) בתמונה המקורית. (ז”א למשל קפסולה במיקום שמאלי עליון בלוח 6×6 מייצג את המידע בתמונה שנמצא בפינה שמאלית עליונה)
- השניה נקראת DigitCaps מכילה 10 קפסולות שכל אחת מחזירה וקטור
ממימד 16 (מחושבים באמצעות אלגוריתם Routing). קפסולות אלו לא מחזירות וקטורי פרדיקציה כי אין שכבה שלישית במימוש זה. (התרשים לא מראה את ה dynamic routing על אף שהינו חלק מהרשת)
מה שקצת מבלבל פה זה שמשתתפים פה באימון משתנים נוספים שכדאי שנשים לב אליהם:
כל אחד מהוקטורים יש לסמן כ
(עם מציין לאינדקס האיטרציה) כי למעשה וקטורי r+1 מחושבים על בסיס וקטורי r.
אז מה בדיוק מאמנים פה ? מהי פונקציית ה Loss ?
פונקציית ה Loss מורכבת ממרכיב ה Margin Loss ומרכיב ה Reconstruction Loss.
מרכיב ה Margin Loss מבוסס על עשרת וקטורי המוצא של שכבת הקפסולות השניה (DigitCaps) .
ה- Margin Loss הינו סכום עבור k=0..9 של:
capsule loss function
כאשר Tk=1 אם ורק אם התמונה שהוזנה מכילה ספרה k, והפרמטרים +-m הינם ספים 0.1\0.9 בהתאמה, ו λ=0.5. (ערכים מומלצים לפי המאמר).
משמעות Loss זה בפשטות הינו תתגמל אם Vk מצביעה על הספרה של התמונה שהוזנה ותעניש אם לא.
כמו כן ישנו את מרכיב ה Reconstrucion Loss לו נותנים משקל נמוך והוא למעשה הפרש הריבועים בין התמונה המקורית לבין תמונה משוחזרת.
התמונה המשוחזרת נבנית באמצעות Decoder המורכב משלושה שכבות Fully Connceted שמקבלות את מוצא ה DigitCaps.
מרכיב ה- Reconstruction Loss אינו חובה וכשהוסיפו אותו אכן שיפר תוצאות.
קצת על הקוד
בקישור זה למשל תוכלו למצוא מימוש מלא ב TensorFlow:
https://github.com/naturomics/CapsNet-Tensorflow
הדבר הייחודי ששווה להזכיר שב Dynamic Routing יש לולאה בה כל המשתנים הם חלק מהאימון (ז”א ה Back-Propogation מעדכן אותם) הוא די מבלבל ולא סטנדרטי.
כך למשל ניתן לממש לולאה של טנזורים: (בקישור המימוש קצת שונה)
def condition(input, counter):
return tf.less(counter, 100)
def loop_body(input, counter):
output = tf.add(input, tf.square(counter))
return output, tf.add(counter, 1)
with tf.name_scope(“compute_sum_of_squares”):
counter = tf.constant(1)
sum_of_squares = tf.constant(0)
result = tf.while_loop(condition, loop_body, [sum_of_squares, counter])
with tf.Session() as sess:
print(sess.run(result))
זהו להפעם… אשמח לשאלות ודיונים בנושא!

